30/7/2015, 17:04
Fletninger og Jonesrepræsentationer
Dette er det første af to indlæg, hvis mål er at give en introduktion til Jens Kristian Egsgaards og min artikel om de såkaldte Jonesrepræsentationer, der er på et så lavt niveau, at den kan forstås af alle, der ved lidt om komplekse vektorrum; det vil sige alle, der har haft noget, der svarer til det kursus i lineær algebra, som matematikstuderende har på deres første år.
Jonesrepræsentationer giver i bund og grund en metode til at lave en "fletning" om til en matrix. I bedste fald modellerer disse matricer fletningerne fuldstændigt, således at man kan studere fletninger (hvilket som udgangspunkt er svært) ved at studere matricer (hvilket til gengæld er let). I dette første indlæg definerer vi fletninger og deres Jonesrepræsentationer. I det næste kigger vi nærmere på, hvad de betyder, hvor de kommer fra, hvad de kan bruges til, og hvordan de måske vil revolutionere verden og alt det der.
Fletninger
Så hvad mener jeg, når jeg skriver fletning? En fletning er en samling af et antal strenge, der starter i en samling givne punkter og bevæger sig opad, mens de snor sig rundt om hinanden for til sidst at ende i den samme samling af punkter igen, nu blot højere oppe – vi kræver dog ikke, at en streng ender i det punkt, der ligger over det punkt, som den startede i. Hvis man har lyst til at tænke på fletninger som "virkelige" objekter, kan det være værd at tænke på en fletning som en beskrivelse af, hvordan en samling partikler i planen bevæger sig i tiden, idet retningen "opad" betragtes som tidsudvikling. Derudover kan man også bare vælge at tænke på en fletning som en fletning af hår, eller hvad man nu ellers har lyst til at flette. De følgende billeder viser eksempler på fletninger bestående af fire strenge.
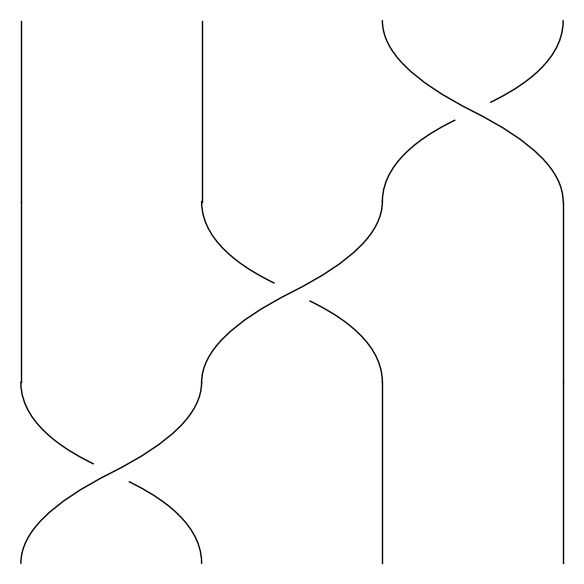
Vi vælger at betragte to fletninger som ens, hvis man kan flytte den ene over i den anden uden at flytte strenge gennem hinanden. Det betyder f.eks., at de følgende to trestrengede fletninger er ens:
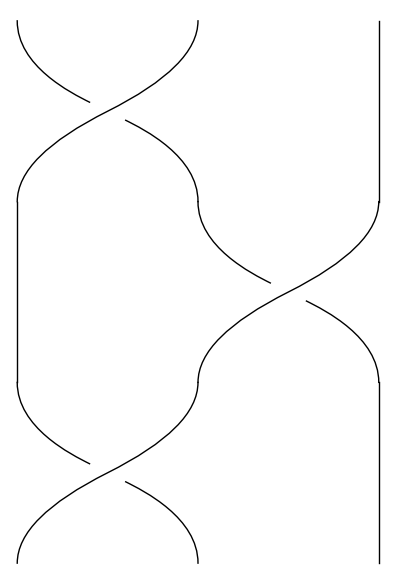
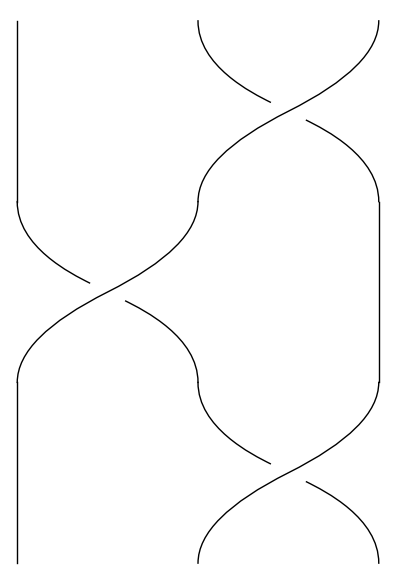
Det eneste krav vi stiller til fletningerne er, at de altid bevæger sig opad; det betyder til gengæld, at enhver fletning med \(n\) strenge kan beskrives på følgende simple vis: Først definerer vi for hvert \(i = 1, \dots, n-1\) en fletning \(\sigma_i\) ved at lade streng nummer \(i\) krydse over streng nummer \(i+1\). De nedenstående tre billeder viser henholdsvis \(\sigma_1\), \(\sigma_2\) og \(\sigma_3\).
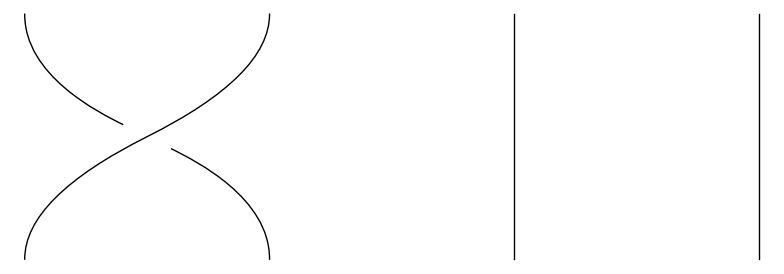
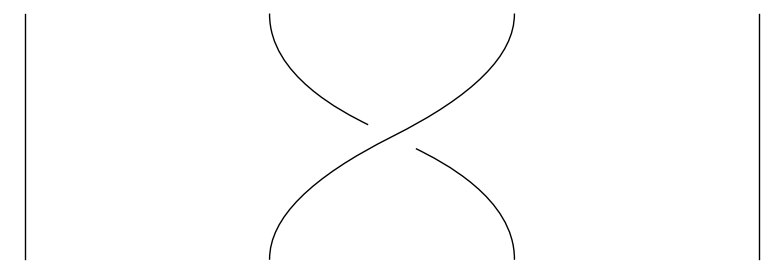
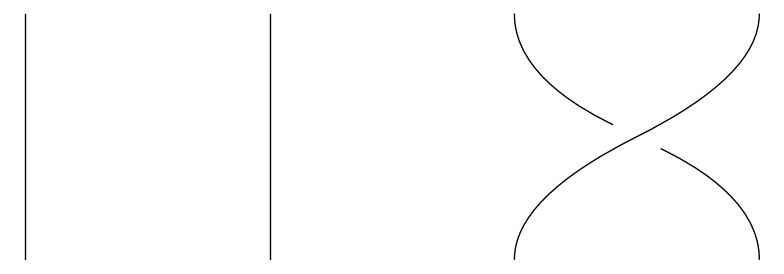
På samme måde definerer vi en fletning \(\sigma_i^{-1}\) ved at lade streng nummer \(i+1\) krydse over streng nummer \(i\). Vi kan nu beskrive en hvilken som helst fletning ved at vælge en samling af \(\sigma_i^{\pm 1}\)'er og stable dem ovenpå hinanden. F.eks. kan følgende fletning beskrives ved 'ordet' \(\sigma_2 \sigma_1 \sigma_3^{-1}\) (læs billedet nedefra og op):
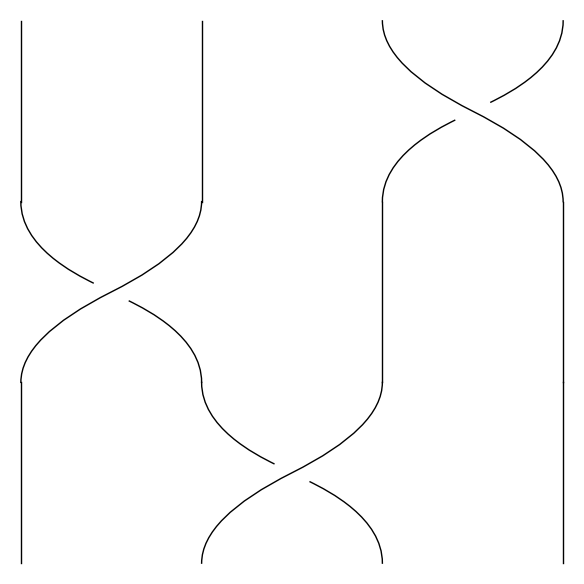
Diagramvektorrum
Vores mål er som sagt at lave fletninger om til matricer. Det gør vi ved først at beskrive en basis for et vektorrum og derefter beskrive, hvad fletningerne skal gøre ved basiselementerne. Vores basiselementer vil blive givet ved en type abstrakte diagrammer.
Tag igen et naturligt tal \(n\) og vælg et tal \(d \in \{0,\dots,n-1\}\) (hvor \(d\) står for dræn), således at \(d\) og \(n\) enten begge er lige eller begge er ulige. Betragt nu et to-dimensionalt kvadrat med \(n\) punkter valgt på toppen og \(d\) på bunden. Et basisdiagram er nu pr. definition et diagram i kvadratet, der forbinder hvert af de \(n+d\) punkter med et andet af punkterne, således at diagrammet ikke har nogen selvgennemskæringer, og således at et punkt fra bunden altid er forbundet til et punkt fra toppen. Her er de to mulige diagrammer for \(n = 4\), \(d = 0\):
For \(n = 4\), \(d = 2\) er der 3 basisvektorer, \(v_1\), \(v_2\) og \(v_3\):
For hvert par \((n,d)\) definerer vi nu et vektorrum \(V^{n,d}\) til at være udspændt af alle diagrammer hørende til parret \((n,d)\). Det vil f.eks. sige, at \(V^{4,0}\) er udspændt af to diagrammer, mens \(V^{4,2}\) er udspændt af tre diagrammer. Med andre ord har vektorrummene dimensioner \(\mathrm{dim} V^{4,0} = 2\) og \(\mathrm{dim} V^{4,2} = 3\). Lidt mere generelt kan man vise, at dimensionen af \(V^{2n,0}\) er givet ved en forskel mellem binomialkoefficienter, \[\dim V^{2n,0} = \binom{2n-1}{n} - \binom{2n-1}{n-2}.\] Dette tal kaldes også det \(n\)'te Catalantal, og for generelle \((n,d)\) gælder en lignende formel.
Jonesrepræsentationer
Vi er nu i stand til at knytte en matrix \(\eta(\sigma)\) til enhver fletning \(\sigma\). Fasthold et naturligt tal \(n\) – antallet af strenge – og vælg et eller andet \(d\) som ovenfor, så vi har et vektorrum \(V^{n,d}\). Tag nu en vilkårlig fletning \(\sigma\). Vi er færdige med vores konstruktion, hvis vi kan definere, for hvert eneste basisdiagram \(v\), en linearkombination \(\eta(\sigma)(v)\) af basisdiagrammer. Her er \(\eta(\sigma)\) den matrix, vi er på jagt efter. Den eksempelforetrækkende læser kan med fordel scrolle lidt ned, idet vi slutter af med et eksempel.
Matricen opstår som følger: Tag diagrammet \(v\) og sæt fletningen \(\sigma\) ovenpå; kald resultatet \(\sigma . v\). Resultatet er ikke et diagram, men det kan vi tvinge det til at blive: Tag et hvilket som helst (komplekst) tal \(A \not= 0\) og fjern alle kryds i \(\sigma . v\) ved at bruge følgende regel til at lave en linearkombination af de to forskellige måder at skabe diagrammer uden selvgennemskæringer:
På denne måde kan vi fjerne alle krydsninger, men der er nu to ting, der kan gå galt: Vi kan risikere at ende med at få to punkter i bunden forbundet, hvilket vi ikke tillod ovenfor, og vi kan risikere at ende med at få en cirkel, der ikke forbinder noget som helst. I det første tilfælde, hvor to punkter i bunden bliver forbundet, løser vi problemet ved at kalde resultatet \(0\); vi fjerner det altså helt fra udregningen. I det andet tilfælde, hvor vi ender med en cirkel, vælger vi at fjerne cirklen og at gange resultatet med tallet \(-A^2 - A^{-2}\).
På nuværende tidspunkt er det nok på plads med et par eksempler på den abstrakte beskrivelse ovenfor. Lad os se på tilfældet \(n = 4\), \(d = 2\). Vi har så de tre forskellige basisdiagrammer \(v_1\), \(v_2\) og \(v_3\), som vi fandt tidligere. Lad os prøve at finde ud af, hvad \(\eta(\sigma_1)\) er, hvor \(\sigma_1\) er den elementære fletning, hvor den første streng krydser over den anden streng. Det vil sige, at \(\sigma_1 . v_1\) ser sådan her ud:
Vi bruger nu vores regel til at fjerne krydset og får, at
I resultatet har vi altså fået noget, der ligner vores oprindelige diagram tilbage, bortset fra at vi nu har en ekstra cirkel i den ene summand, og ifølge ovenstående beskrivelse skal vi fjerne cirklen og gange med \(-A^2 - A^{-2}\). På bundlinjen får vi altså, at
Skrevet med symboler har vi nu fundet, at \[\eta(\sigma_1)(v_1) = (A+A^{-1}(-A^2-A^{-2}))v_1 = -A^{-3} v_1.\] Vi kan lave den samme gymnastik for \(v_2\) og \(v_3\) og her vil man finde, at \(\eta(\sigma_1)(v_2) = A^{-1} v_1 + A v_2\), og at \(\eta(\sigma_1)(v_3) = A v_3\). Sætter man det hele sammen, har vi udregnet, hvad \(\eta(\sigma_1)\) gør ved vektorrummets tre basisvektorer \((v_1,v_2,v_3)\). Med andre ord er \(\eta(\sigma_1)\) i denne basis givet ved
\[\eta(\sigma_1) = \begin{pmatrix} -A^{-3} & A^{-1} & 0 \\ 0 & A & 0 \\ 0 & 0 & A\end{pmatrix}.\]
Idet hele udregningen er så algoritmisk, bør det ikke være den store overraskelse, at det er let at lokke en computer til at udføre den i stedet, og dette værktøj gør præcis det.
Et åbent spørgsmål
Nu hvor vi har brugt lidt tid på at definere matricerne \(\eta(\sigma)\), er det på sin plads at nævne, at vi faktisk ikke har vanvittigt godt styr på dem, til trods for at de er så relativt lette at definere. Et naturligt spørgsmål er, om vi har mistet information ved at kigge på matricerne i stedet for fletningerne. Det er netop spørgsmålet om, hvorvidt samlingen af \(\eta\)'er for forskellige \(d\) giver en injektiv afbildning eller ej. Dette kan til gengæld formuleres som følger: "Fasthold et \(n\). Givet et \(\sigma\) sådan at der for alle \(d\) gælder, at \(\eta(\sigma) = \mathrm{Id}\), hvor \(\mathrm{Id}\) er identitetsmatricen, er det så sandt, at \(\sigma\) selv er den trivielle fletning, hvor alle strengene er lodrette?" Dette viser sig at være sandt, hvis \(n = 2\) og \(n = 3\), men for alle større værdier af \(n\) aner vi ikke, hvad der foregår. Selv det umiddelbart simple tilfælde \(n = 4\) (som sikkert ikke er spor simpelt) kunne det være fedt at få afklaret.
Et par historiske bemærkninger
Samlingen for alle \(d\) af afbildningerne \(\eta\), der tager en fletning og giver en matrix er hvad, der kendes som Jonesrepræsentationen. Jonesrepræsentationerne er opkaldt efter Vaughan Jones, der studerede dem og deres egenskaber i slutningen af 80'erne. Det var blandt andet for dette arbejde, at han i 1990 blev tildelt Fieldsmedaljen; den mest prestigefyldte matematikpris.
I det specielle tilfælde, hvor \(d = n - 2\) (hvilket f.eks. er det, vi kiggede på i eksemplet ovenfor), kaldes tilknytningen af matricer til fletninger for Buraurepræsentationen, efter Werner Burau der studerede dem i 1930'erne. Matematikere, der er stødt på Buraurepræsentationen før, vil nok kende dem som repræsentationen af fletninger på hvad der kaldes homologien af det uendelige parkeringshus (se konstruktionen på animationen til højre). Hvis man i dette hus ganger en homologicykel med faktoren \(A^{\pm 4}\), svarer det til at flytte cyklen op og ned i huset, hvilket til dels kan forklare, hvor dette lidt mystiske komplekse tal kommer ind i billedet. Hvad betydningen af \(A\) er, ser vi også nærmere på i næste indlæg, der nu er at finde her.
Kommentarer
Ingen kommentarer endnu.
Tilføj kommentar
For at undgå for meget spam på siden skal du logge ind for at tilfæje en kommentar. Det kan du gøre nedenfor, eller du kan lave en bruger, hvis du ikke har en allerede. Du kan også bruge dit fotologin her.